Differentiable Particle Filtering
Background
Particle filtering1, and more broadly sequential Monte-Carlo, are a family of classical algorithms for Bayesian inference that draw samples from the posterior distribution of a hidden variable given a sequence of noisy data. However, parameter inference for sequential hidden variable systems, often known as ‘state-space models’ is challenging and established techniques are limited to models of specific algebraic forms or with a low number of parameters. To learn to more complex models, such as those parameterised by neural networks, and general objective functions, such as the error in the estimated mean of the particle filter, we employ powerful first order optimisation techniques. However, these require access to the derivative of the particle filtering algorithm which, as it is a stochastic program, is not defined. Particle filters modified such that they return a useful surrogate derivative estimate are known as ‘differentiable particle filters (DPFs)’.
Implementation
In collaboration with researchers at the University of Edinburgh we have developed a python package for differentiable particle filtering (PyDPF)2. Our package is designed with flexibility in mind, we provide a convenient framework for developing sequential Monte-Carlo algorithms for use with the popular auto-differentiation package PyTorch. We provide a standardised pattern for defining state-space models, using familiar PyTorch Module classes, that allows them to be used with any algorithm defined in PyDPF. We implement many of the currently published filtering algorithms, but employ a highly modular design allowing an ease of development for new algorithms and variants.
Pypi distribution coming soon.
Differentiable Interacting Multiple Model Particle Filtering
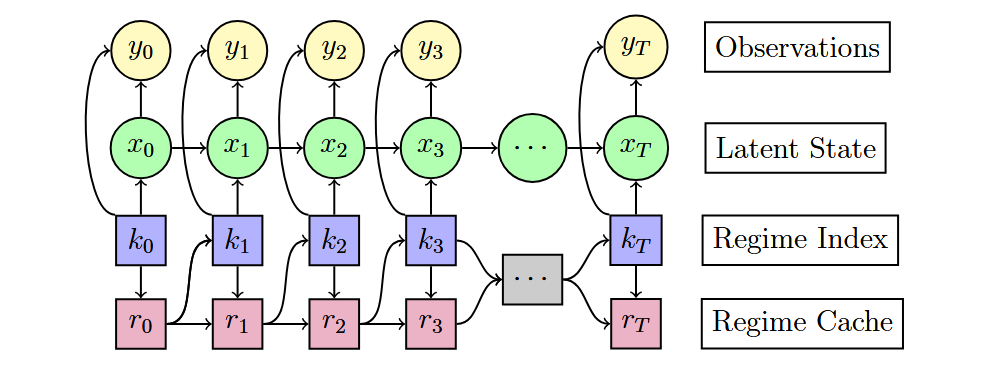
An area that has received specific attention in the filtering literature is regime-switching models sometimes referred to as ‘jump Markov models’, in which the system may exhibit one of a finite set of models at any time-step, but the model may discontinuously and randomly change to another in the finite set. Examples of behaviour that may be modelled in this way include the position of a person switching between modes of transport or a financial market reacting to news. In our paper3 we extend a popular classical approach4 to a deep learning setting, and generalise upon and improve the accuracy of previous machine learning approaches5. We also provide new theoretical results and develop a new gradient estimator that can be applied more broadly in DPFs.